Finding the Diameter of a Binary Tree using Depth-First Search

Solving the Diameter of Binary Tree Problem with Recursion

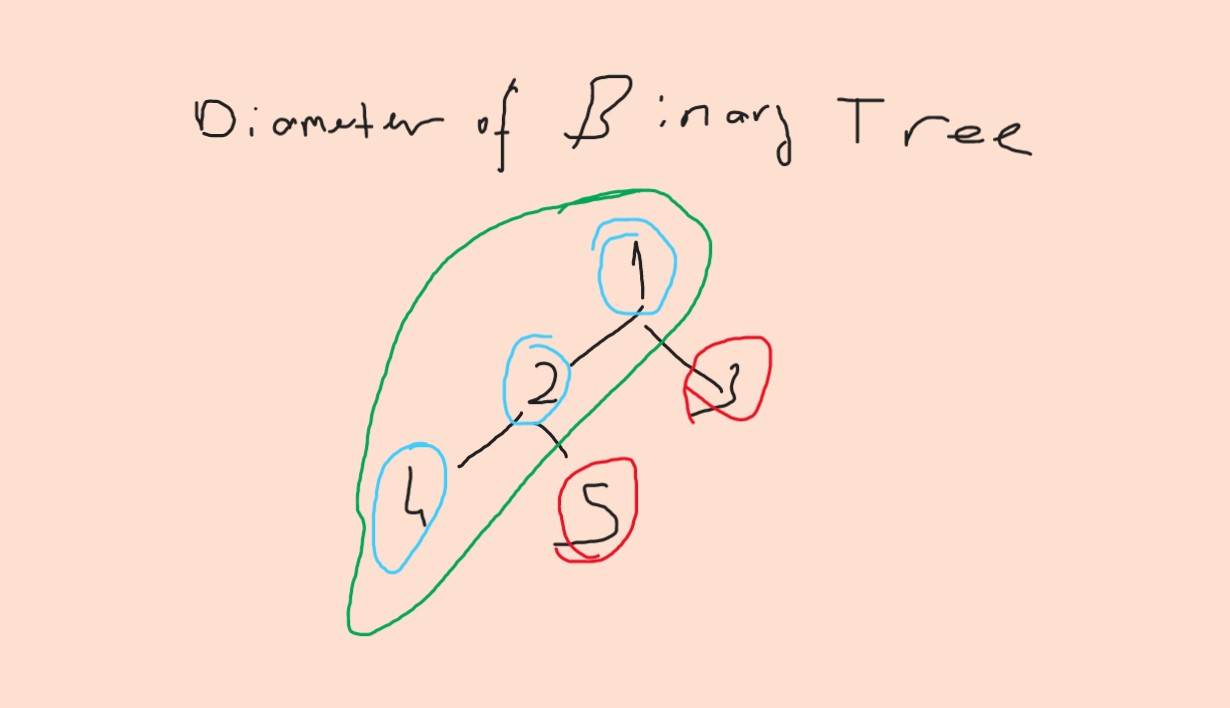
The “Diameter of Binary Tree” problem asks us to find the length of the longest path between any two nodes in a binary tree. This path may or may not pass through the root of the tree. The length of a path is defined as the number of edges between the nodes.

To solve this problem, we can use a recursive approach that traverses the tree depth-first and keeps track of the maximum diameter seen so far. Here’s how the algorithm works:

Define a function dfs(node) that takes a node as input and returns the depth of the deepest leaf node in the subtree rooted at node, as well as the maximum diameter seen so far. We can keep track of the maximum diameter using a variable max_diameter.

Inside dfs(node), recursively call dfs() on the left child (if it exists) and the right child (if it exists) of node. This will explore the left and right subtrees of node, respectively.

Once we have the depths of the left and right subtrees, we can compute the depth of the deepest leaf node in the subtree rooted at node by taking the maximum depth of the left and right subtrees and adding 1 (since node is one level deeper than its children).

We can also compute the maximum diameter seen so far by taking the sum of the depths of the left and right subtrees (if they exist) and comparing it to the current max_diameter. If the sum is greater than max_diameter, we update max_diameter to the sum.

Return the depth of the deepest leaf node in the subtree rooted at node and the maximum diameter seen so far to the parent of node.

Here’s the Python code for the dfs() function:

def dfs(node):
    # If the current node is None, return 0
    if not node:
        return 0
    
    # Recursively calculate the depths of the left and right subtrees
    left_depth = dfs(node.left)
    right_depth = dfs(node.right)
    
    # Update the maximum path seen so far
    self.diameter = max(self.diameter, left_depth + right_depth)
    
    # Return the maximum depth of the left and right subtrees plus one
    return max(left_depth, right_depth) + 1

We start by checking if node exists (i.e., is not None). If it doesn’t, we return a depth of 0 and a diameter of 0 to the parent. This is the base case of the recursion.

If node exists, we recursively call dfs() on its left and right children, and assign the returned depths and diameters to left_depth, left_diameter, right_depth, and right_diameter, respectively.

We then compute the diameter of the subtree rooted at node as the sum of the depths of the left and right subtrees.

Next, we update max_diameter if the current diameter is greater than it.

Finally, we return the depth of the deepest leaf node in the subtree rooted at node (which is the maximum depth of the left and right subtrees plus 1), as well as the maximum diameter seen so far.

To use the dfs() function to solve the problem, we simply call it on the root of the binary tree and return the maximum diameter seen:

so full code:

class Solution:
    def diameterOfBinaryTree(self, root: TreeNode) -> int:
        # Define a helper function to calculate the depth of each node
        def dfs(node):
            # If the current node is None, return 0
            if not node:
                return 0
            
            # Recursively calculate the depths of the left and right subtrees
            left_depth = dfs(node.left)
            right_depth = dfs(node.right)
            
            # Update the maximum path seen so far
            self.diameter = max(self.diameter, left_depth + right_depth)
            
            # Return the maximum depth of the left and right subtrees plus one
            return max(left_depth, right_depth) + 1
        
        # Initialize diameter to 0
        self.diameter = 0
        
        # Call the dfs() function on the root node
        dfs(root)
        
        # Return the final value of diameter
        return self.diameter

Call dfs(1):
- Call dfs(2):
  - Call dfs(4):
    - Return 0 (node 4 has no children)
  - Call dfs(5):
    - Return 0 (node 5 has no children)
  - Return max(0, 0) + 1 = 1 (depth of node 2)
- Call dfs(3):
  - Return 0 (node 3 has no children)
- Update diameter to max(diameter, 1 + 0) = 1 (since the path 4-2-1-3 has length 3)
- Return max(1, 0) + 1 = 2 (depth of node 1)